[Most Recent Entries] [Calendar View] [Friends]
Below are the 20 most recent journal entries recorded in
Almost certainly not Johnny Depp.'s InsaneJournal:
| Friday, October 13th, 2023 | |
| 7:24 pm | theweaselking @ 2017-06-17T13:41:00 Trump supporters are so stupid that now they're attacking organisations with "Shakespeare" in the name. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4803 |
| 7:24 pm | theweaselking @ 2017-06-14T09:47:00  Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4803 |
| 7:24 pm | CANDY. COATING. Overkill Software is giving away 5 million copies of Payday 2. Free. It doesn't come with any of the DLC, but: 1) you don't *need* any of the character/weapon/mask DLC to have a great time 2) all the heist DLC is shared - so if you join my game and I have a DLC heist, you can play it even if you don't have the DLC Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4803 |
| 7:24 pm | theweaselking @ 2017-06-05T12:50:00 Gay Vultures Become Proud Daddies After Hatching Abandoned Egg Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4802 |
| 7:24 pm | On the topic of films. Wonder Woman was good. Quite good. While calling it "the best DC movie ever" is damning with faint praise, it was *actually good*. Like, "comparable to several Marvel movies" good. Not just "good for a comic book movie" and DEFINITELY not merely "the best DC movie ever", actually good, compared to other movies that are good, not just "good for X". Wonder Woman appears to have finally figured out that if you make a movie *not suck*, it will get good reviews and attract audiences. However, it's DC and Warner Brothers: The odds of them doing that *again* for Justice League are extremely long, and that makes me sad. In the mean time, Wonder Woman was really good. Go see it, encourage DC/WB to try to make more movies that aren't god-awful. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4802 |
| 7:24 pm | Roger Waters has opinions.  Taken in Kansas City at the first concert of Roger Waters' current tour. Related Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4802 |
| 7:24 pm | theweaselking @ 2017-05-25T20:10:00 40! Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4802 |
| 7:24 pm | theweaselking @ 2017-05-07T16:27:00 It's almost as if, outside the USA? Nazis and Nazism are unpopular. 37% of France is a depressingly large chunk of deeply shitty garbage people, though. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4801 |
| 7:24 pm | A brief comment on Georgia. I want to talk about these election results from yesterday. 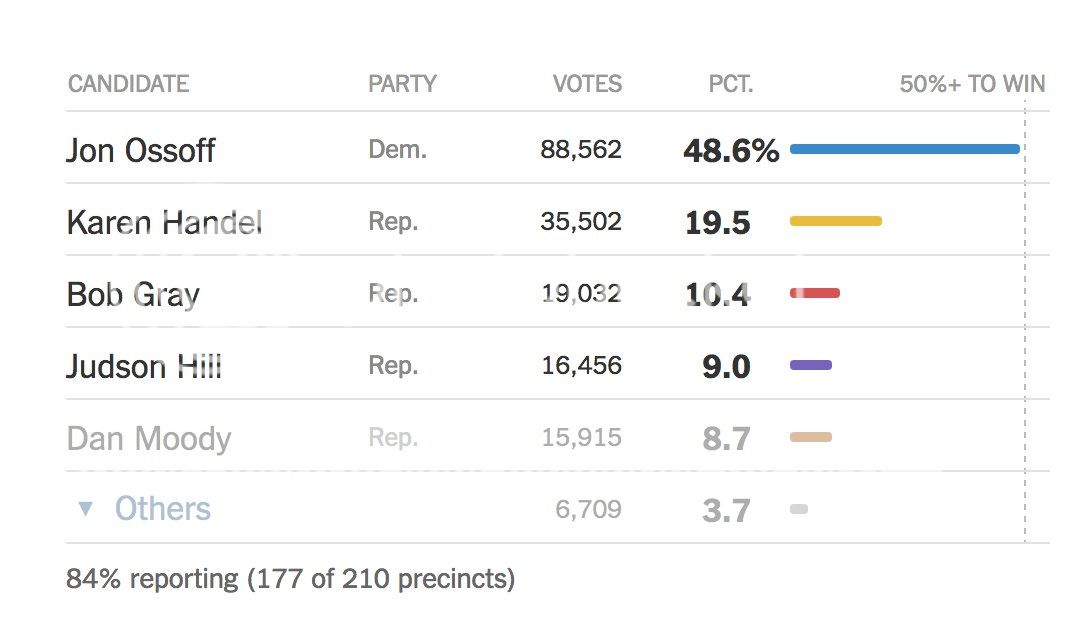 And I'm not going to remark on the Democrat taking such a big share of votes, or anything like that. I just want to know if anyone else noticed that PENNYWISE THE DANCING CLOWN is apparently a Republican congressional candidate? Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4801 |
| 7:24 pm | Body Count: No Lives Matter. This is, as the saying goes, basic shit. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4801 |
| 7:24 pm | Rollover day. Today marks the start of year 13. Normally I'd be all "death ray! Comment statistics! posts!" but honestly, I just don't care this year. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4801 |
| 7:24 pm | I love this puzzle. 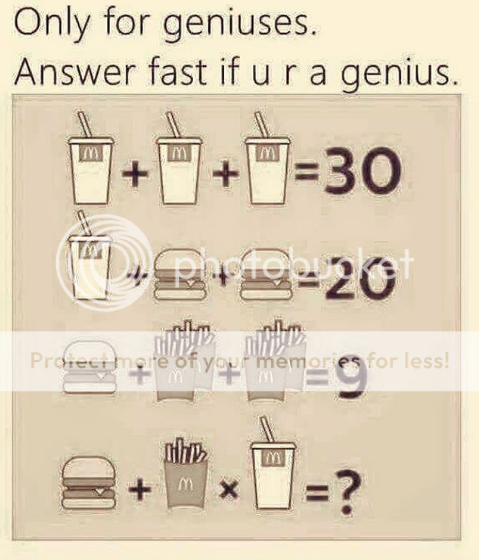 It's surprisingly tricky. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4801 |
| 7:24 pm | For the people interested: This year's Hugo Award finalists were announced about an hour ago. It's a good list this year, only a couple of real turds and some truly excellent options. Best Dramatic Long: HIDDEN FUCKING FIGURES. That one is winning OR ELSE I WILL TURN THIS CAR AROUND I'm just saying. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4800 |
| 7:24 pm | Hoversheeps go whirrrrrrrrrrrrr  (apparently originally from here, but this site is awful and I can't find it.) See also:  Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4800 |
| 7:24 pm | Help me lazyweb. Yikes, I haven't made a post in a while. OK, first New!Content! in a week.... tell me about music players. Yes, yes, "a smartphone", I know that one. Phones *suck* as music players for me because the controls are on a touchscreen, which tends to lock, making them COMPLETE ASS while driving. I want a device that plays music with: 1) a standard stereo out that will go to my car's stereo in. 2) at least 30GB of storage 3) CONTROLS THAT I CAN OPERATE ONE-HANDED WITHOUT LOOKING AT THEM. I don't care if I have to look at it to select a specific track or podcast or something, but I want to be able to reach down from the gearshift and, at the very least, manage play/pause/forward/back, by touch alone. 4) Controls that let me choose specific tracks, playlists, podcasts, etc if I *am* looking at them. Nice to have: Syncs to the old version of iTunes that I've neutered down to the way I like it and that I use to sort my music. Basically, the perfect device that works exactly the way I want it is the 6th generation iPod Classic, which, since it's a perfectly good tool that fills an important niche that the iPhone doesn't, Apple no longer makes it. You can get them on eBay for, like, $800 and fuck that. It's actually the device I've got right now, but despite lasting WAY longer than any Apple product normally does, it's starting to fail on me (it crashes and the battery life isn't great any more). So. I'm not spending $800 for a used device, or even for a "new in box" Apple device manufactured in 2014. Apple's batteries are legendary, and not in a good way - my device living as long as it has makes it an outlier. Who makes a device these days, that plays music through a stereo jack, with controls that can be operated by touch? Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4800 |
| 7:24 pm | theweaselking @ 2017-03-21T22:56:00 Holy fuck: Dolby's last patent on Dolby Digital expired last night. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4799 |
| 7:24 pm | Holy crap:  Imagine being *such a dipshit* that you side with spammers and telemarketers and other malware vendors. Of course, Chuck Asay loves telemarketers because they're the only time a human will talk to him. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4799 |
| 7:24 pm | theweaselking @ 2017-02-22T13:46:00 US border turns back Canadian man based on the contents of his dating profile. Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4799 |
| 7:24 pm | theweaselking @ 2017-02-22T09:19:00  Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4798 |
| 7:24 pm | theweaselking @ 2017-02-21T13:59:00  Crossposted from Dreamwidth. Original at http://theweaselking.dreamwidth.org/4798 |